Subject pool and scanning
A total of 137 children ages 3 to 11 years old were recruited using fliers and word-of-mouth. The age limits were determined based on (1) developmental maturity sufficient to stand still for 15 seconds at a time and (2) minimal evidence of puberty. Figure 1 shows the distribution of stature and body weight versus age in months in the subject pool. Growth curves from the U.S. National Center for Health Statistics for weight and stature (5th, 25th, 75th and 95th percentile) are overlaid on the charts.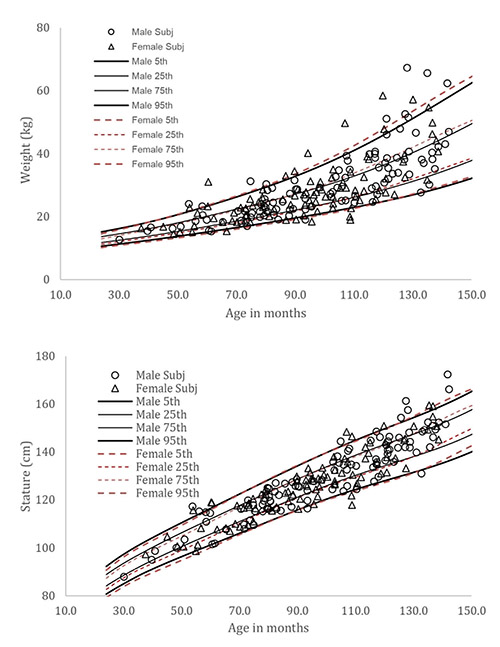
Figure 1. Distribution of stature and body weight versus age in months in the subject pool. Growth curves from the U.S. National Center for Health Statistics (2001) are shown for reference.
Surface measurement was conducted using a VITUS XXL laser scanner and reconstruction software ScanWorX (Human Solutions). Hardware and software system performance was verified prior to each day of testing by scanning a 100-mm diameter pole and verifying the circumference measurement. In general, the system accuracy is approximately 2 mm, depending on the location within the scan volume.Statistical Analysis
A principal component analysis (PCA) was conducted using the methods described in Reed and Parkinson (2008). In brief, the coordinates of the mesh vertices are flattened to create a geometry vector for each scan standardized by fitting a template. The 27 standard anthropometric variable values were appended to each vector along with the 3D coordinates of 138 surface landmarks and estimated joint center locations. PCA was conducted on these geometry matrices to find the linear projection that reduces dimension of the matrix while variance in the data is well preserved. The first 60 PC scores for the matrices were retained from the PCA, representing a statistically significant (p<0.05) amount of variance in the geometric data.Following the methods described in Reed and Parkinson (2008), a linear regression analysis was conducted to associate the projected PC scores with subject characteristics such as stature, body mass index (body mass in kilograms divided by stature in meters squared), and the ratio of erect sitting height to stature (SHS) as predictors.
Results
The statistcal body shape model was built based on the fitted models. A range of body sizes and shapes generated using the resulting SBSM model is shown in Figure 2. Predictors such as stature (100 ~ 160 cm) and BMI (11 ~ 27 kg/m2) vary over approximately the range in the subject pool along the vertical and horizontal axes of the plot, respectively. The created models readily capture the different effects of each predictor. Note that the change in body proportions was also observed along with stature, which is a predominant visual cue to age.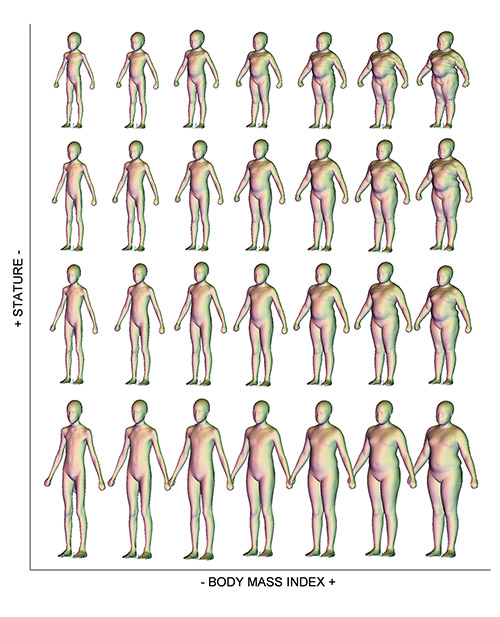
Figure 2. Range of body sizes and shapes. BMI varies along the horizontal axis (11 ~ 27 kg/m2) and stature effects vary along vertical axis (100 ~ 160 cm).
The explanatory power of the model's anthropometric predictors such as stature, BMI, and SHS was validated by comparing the scan data with created models based on actual anthropometric data of the same subjects. Figure 3 shows the result of this comparison. Errors were coded with a heat map (ranged 0 mm to 50 mm) and were evaluated only for the torso to remove the effect of limb posture variance. The residual variance of the regression model across subjects was computed, and the mean error was 10.4 mm, and 95th percentile error was 24.0 mm. Error variance was largest in the shoulders, upper hips, and crotch, and lowest in the abdomen.
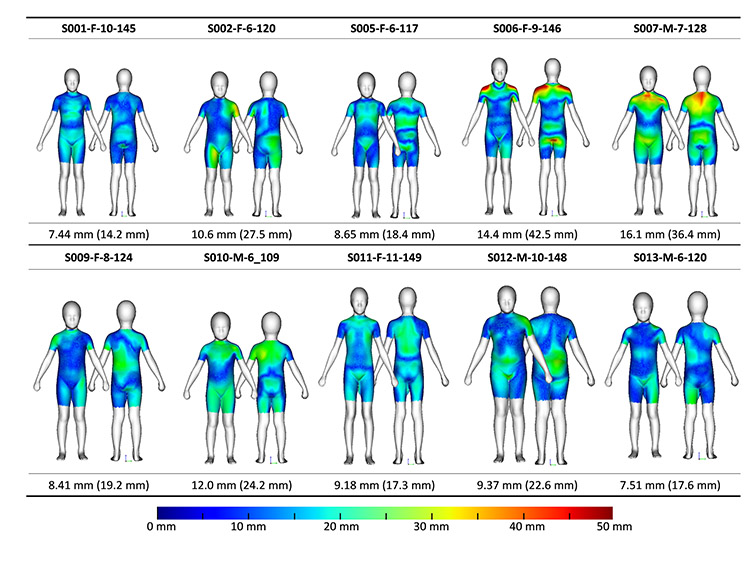
Figure 3. Sampled results of comparisons between fitted template models and reconstructed data using anthropometric predictors such as stature, BMI and SHS.
Applications
The statistcal body shape model presented here is broadly applicable and can be readily extended to a wide range of applications. We have applied the model to fitting low-resolution data from Microsoft Kinect, demonstrating the rapid generation of avatars from Kinect data along with accurate prediction of standard anthropometry (Park and Reed 2014, Park et al. 2015). We expect that the model will be useful for generating anthropometric specifications for human surrogates used for safety applications, such as crash test dummies and finite-element models used for crash simulation. For these applications, the desired body size is usually specified using only a few variables, typically stature, body weight, and erect sitting height. We expect the model to be integrated into commercial ergonomics software, such as the Jack human modeling software, in the same manner as we have demonstrated using adult SBSMs (Reed et al. 2014). We also anticipate that this or similar SBSMs may be useful for stochastic investigation of the performance of protective equipment, which currently is performed using a small number of body forms. Likewise, clothing fitting simulations might be enhanced by the availability of a well-validated parametric model.Related Articles
Pagano, B., Parkinson, M.B., and Reed, M.P. (2015). An updated estimate of the body dimensions of U.S. children. Ergonomics. 10.1080/00140139.2014.1000392.
Park, B-K, Lumeng, J.C., Lumeng, C.N., Ebert, S.M., and Reed, M.P. (2014). Child body shape measurement using depth cameras and a statistical body shape model. Ergonomics, 58(2):301-309. 10.1080/00140139.2014.965754.
Park, B-K. and Reed, M.P. (2014). Rapid generation of custom avatars using depth cameras. Proc. 3rd International Digital Human Modeling Conference. Tokyo, Japan.
Reed, M.P., Raschke, U., Tirumali, R., and Parkinson, M.B. (2014). Developing and implementing parametric human body shape models in ergonomics software. Proc. 3rd International Digital Human Modeling Conference. Tokyo, Japan.
Reed, M. P., & Parkinson, M. B. (2008). Modeling variability in torso shape for chair and seat design. In ASME 2008 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (pp. 561-569). American Society of Mechanical Engineers.